Examples

The first example is a model for the human thigh-bone (femur). The tetrahedral mesh, shown in the figure below, was generated by the Institute of Applied Mechanics (FAM - Fachgruppe Angewandte Mechanik / web-site: http://fam.uni-paderborn.de) at the University of Paderborn, Germany, and put at the author's disposal, which is gratefully acknowledged. Clearly visible are the head (caput femoris), the neck (collum femoris) and the trochanter minor and major (the moon-like elevation separating the neck from the body of the femur). Only half of the femur was modeled. The mesh contains about 120,000 degrees of freedom.

Tetrahedral mesh for the femur (back view of the right femur)

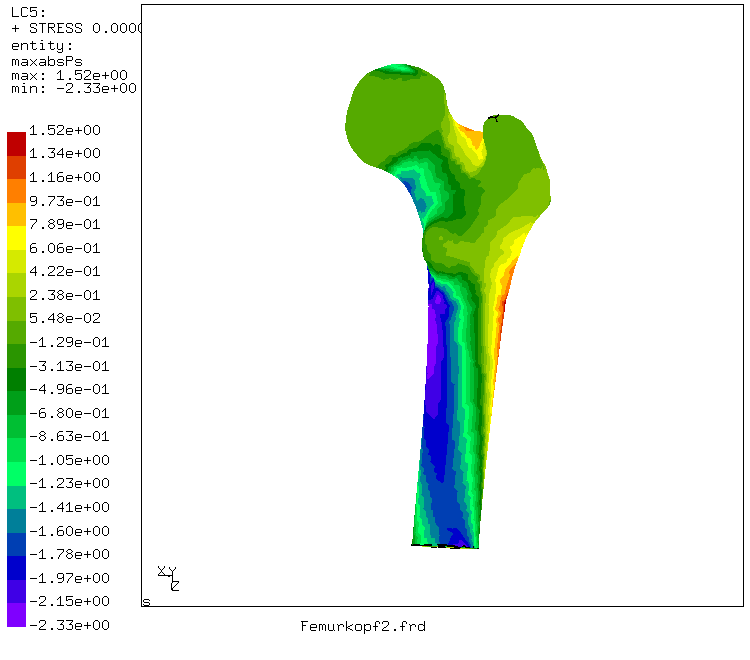
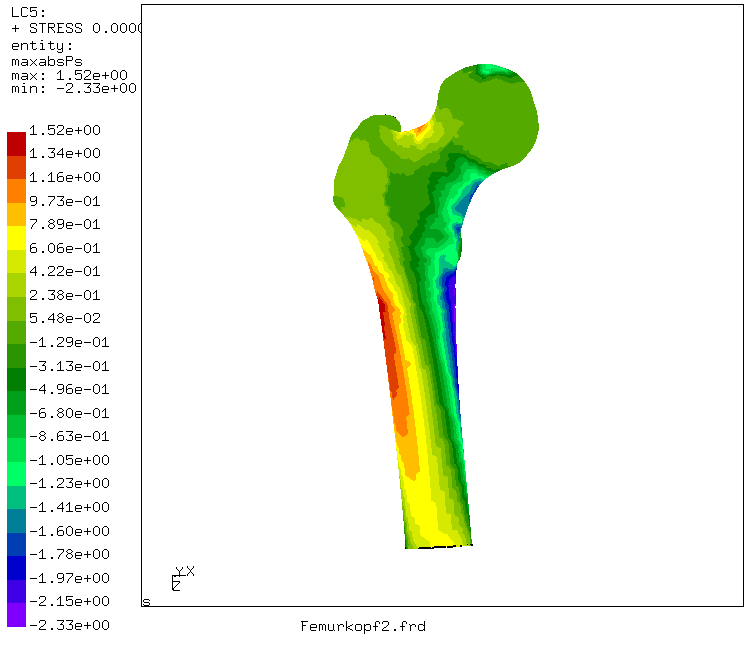
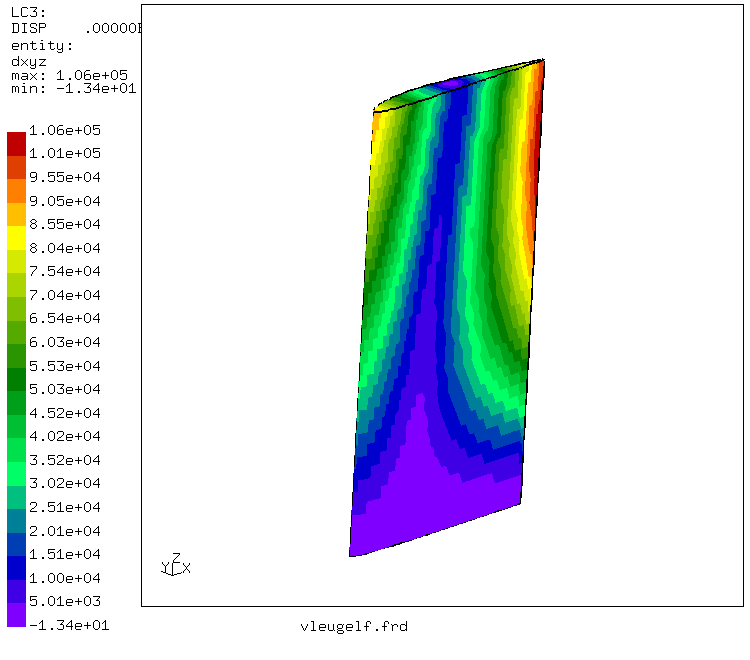
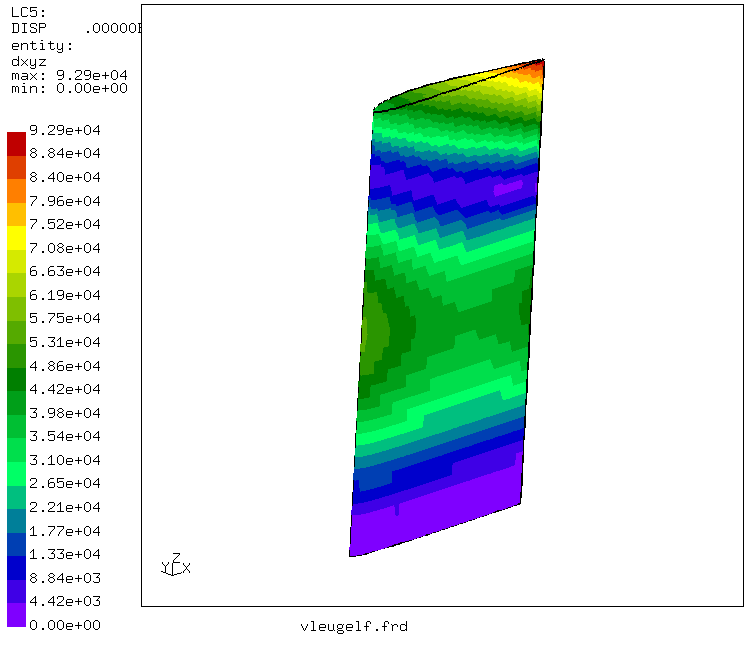
The bone material (substantia compacta as well as the substantia spongiosa) was modelled as one and the same linear elastic isotropic material, the cavitas medullaris is void. A force of 300 N was applied on the head of the femur in the direction of the knee. This force corresponds to about half the weight of an average man above the thights and its direction fits a human being standing on both legs in an upright position. The lower end of the model was fixed in all directions. Due to the shape of the femur, this force (applied as a distributed pressure) leads to internal bending moments. The corresponding tensile and compressive stresses reach values of about 3 MPa. This is illustrated in the next two figures, where the maximum principal stress is plotted in two different views.

Highest principal stress - back view

Highest principal stress - front view

The following table gives an impression of the CPU-time needed for a linear static calculation of the above model on different platforms:

Solver	Platform	CPU-time
Iterative, scaling	Pentium 200 MHz	86'
Iterative, Cholesky	Pentium 200 MHz	45'
SPOOLES	Athlon 700 MHz	17'
Iterative, scaling	Athlon 700 MHz	14'
Iterative, Cholesky	Athlon 700 MHz	7'

The next example is a NACA profile translated along the z-axis, thus generating an artificial wing. The wing was fixed on one end (in all directions). An eigenmode analysis was performed and the ten lowest eigenmodes and frequencies were calculated. The figures below show the lowest torsion mode and a higher bending mode.

Displacements of the lowest torsion mode

Displacements of a bending mode with two nodes

The following example is NAFEMS benchmark 3DNLG-9: large elastic deflection of a pinched hemispherical shell. The structure is a hemispherical shell with a circular hole at its pole. The loading consists of two compressive and two tensile forces applied in alternating mode every 90 degrees along the lower boundary of the shell. The radius of the shell is 10 m, its thickness is 40 mm. It was meshed using C3D20R elements, which prove to be very well suited for such thin structures. The following table compares the CALCULIX results with a reference solution (also obtained by FE):

Load	A (CALCULIX)	A (reference)	B (CALCULIX)	B (reference)
40	-3.24	-3.26	2.31	2.32
60	-4.29	-4.34	2.79	2.82
100	-5.78	-5.90	3.35	3.41

Displacement in the load introduction points A and B (in m)

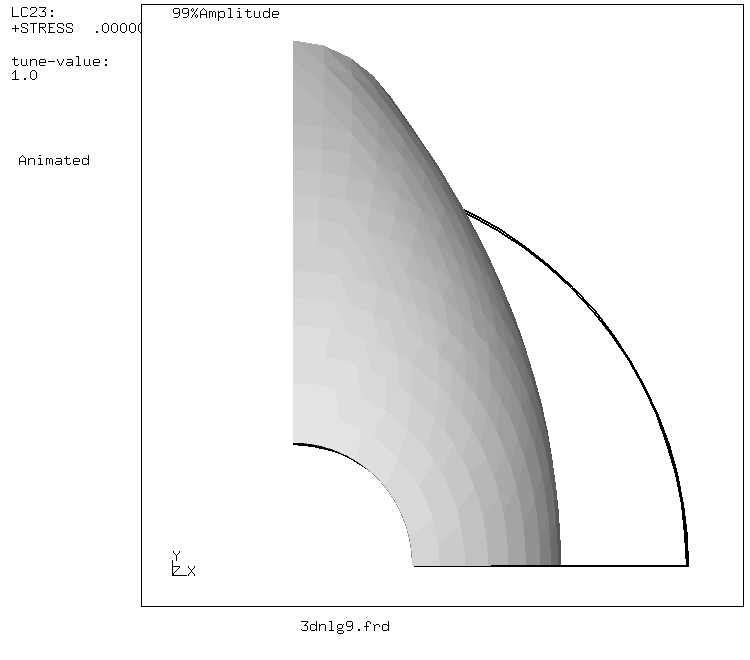
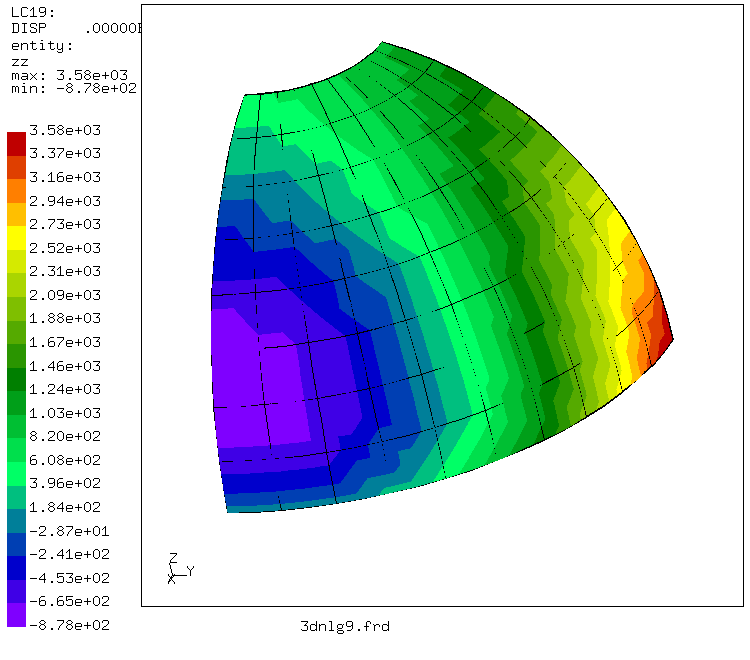
The following figures give an overview of the total deformation and the deformation in the direction of the symmetry axis. The deformations are about half the radius of the shell (large deformation). There was only one layer of elements across the thickness of the shell (1872 degrees of freedom in total). This example shows that the use of 20-node brick elements with reduced integration can also be advantageous for thin shells.

Deformed shell (real displacements)

Displacement in z-direction (in mm)

The last example is a nonlinear buckling problem. A cylindrical shell segment is fixed by hinges on its straight sides and loaded by a point force in the middle. As the force increases, the shell buckles and finds a new equilibrium configuration. This is illustrated in the figure underneath: the line contours show the original geometry, the shaded form the buckled configuration.

Shell before and after buckling

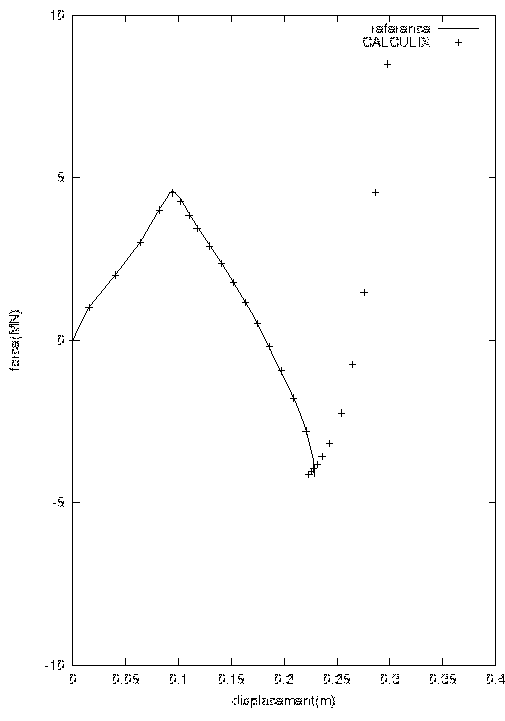
The next figure shows the force versus the displacement in the middle of the shell. The calculation was at first force controlled. Both force and displacement increase up to the buckling of the shell. At this point no convergence was obtained any more, and the calculation was pursued in a displacement controlled fashion. During buckling the force decreases and reaches negative values, i.e. a tensile force has to be exerted to maintain the shell in these intermediate configurations. Then, the force is still negative but increases again. At the minimum value of the force the curve seems to exhibit a kink. Up to this point CALCULIX and the reference solution agreed. Only at the minimum a small difference is observed, and the reference solution (same calculation with a commercial finite element program) stops due to lack of convergence. CALCULIX did not meet this difficulty, and continues its calculation. Now, the force increases in a sort of quadratic fashion, crosses the zero force line (equilibrium in the buckled configuration) and continues this course till the end of the calculation. This seems reasonable, since a new stable configuration has been reached. This calculation shows that one layer of 20-node brick elements is a viable alternative to the use of shell elements and that CALCULIX is able to perform highly nonlinear calculations.

Force versus displacement in the middle of the shell

Legal Disclosure
Privacy Policy

Back to previous page